Compute Distributional Statistics from a Discrete Random Variable
back to Fan's Dynamic Assets Repository Table of Content.
Contents
function [ds_stats_map] = fft_disc_rand_var_stats(varargin)
FFT_DISCT_RAND_VAR_STATS compute mean, sd, percentiles
Model simulation generates discrete random variables, to analyze, need to calculate various statistics
Statistics include:
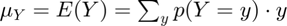
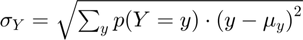
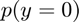
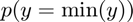
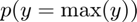
- percentiles:
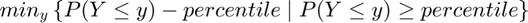
- fraction of outcome held by up to percentiles:
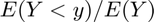
@param st_var_name string name of the variable (choice/outcome) been analyzed
@param ar_choice_unique_sorted array 1 by N elements in the sample space of the discrete random variable ordered. Unique consumption values ordered. Unique asset choices ordered. etc.
@param ar_choice_prob array 1 by N probability mass function associated with each element ar_choice_unique_sorted
@param ar_fl_percentiles array 1 by M some vector of percentiles (0 to 100) that we would like to compute based on the discrete random variable's probability mass function and x values.
@return ds_stats_map container various distributional statistics
@example
% run function st_var_name = 'binom'; [ds_stats_map] = fft_disc_rand_var_stats(st_var_name, ar_choice_unique_sorted, ar_choice_prob, ar_fl_percentiles); % retrieve scalar statistics % fl_choice_mean = ds_stats_map('fl_choice_mean'); fl_choice_sd = ds_stats_map('fl_choice_sd'); fl_choice_prob_zero = ds_stats_map('fl_choice_prob_zero'); fl_choice_prob_max = ds_stats_map('fl_choice_prob_max'); % retrieve distributional array stats ar_choice_percentiles = ds_stats_map('ar_choice_percentiles'); ar_choice_perc_fracheld = ds_stats_map('ar_choice_perc_fracheld');
Default
use binomial as test case
fl_binom_n = 30; fl_binom_p = 0.3; ar_binom_x = 0:1:fl_binom_n; % f(x) ar_choice_prob = binopdf(ar_binom_x, fl_binom_n, fl_binom_p); % x ar_choice_unique_sorted = ar_binom_x - 10; % percentiles of interest ar_fl_percentiles = [0.1 1 5:5:25 35:15:65 75:5:95 99 99.9]; % display st_var_name = 'binom'; % display bl_display_drvstats = true; % default default_params = {st_var_name ar_choice_unique_sorted ar_choice_prob bl_display_drvstats ar_fl_percentiles};
Parse Parameters
[default_params{1:length(varargin)}] = varargin{:};
[st_var_name, ar_choice_unique_sorted, ar_choice_prob, bl_display_drvstats, ar_fl_percentiles] = default_params{:};
f(y), f(c), f(a): Compute Scalar Statistics for outcomes
Compute these outcomes:
- mean:
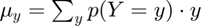
- sd:
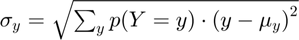
- prob(outcome=0):
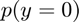
- prob(outcome=max(outcome)):
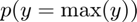
% Mean of discrete random variable fl_choice_mean = ar_choice_prob*ar_choice_unique_sorted'; % SD of discrete random variable fl_choice_sd = sqrt(ar_choice_prob*((ar_choice_unique_sorted'-fl_choice_mean).^2)); % Coef of Variation of discrete random variable fl_choice_coefofvar = fl_choice_sd/fl_choice_mean; % min of y from policy function, p(y) might be 0 fl_choice_min = min(ar_choice_unique_sorted); % max of y from policy function, p(y) might be 0 fl_choice_max = max(ar_choice_unique_sorted); % prob(outcome=min(outcome)), fraction of people not saving for example fl_choice_prob_min = sum(ar_choice_prob(ar_choice_unique_sorted == min(ar_choice_unique_sorted))); % prob(outcome=0), fraction of people not saving for example fl_choice_prob_zero = sum(ar_choice_prob(ar_choice_unique_sorted == 0)); % prob(outcome<0), fraction of people borrowing fl_choice_prob_below_zero = sum(ar_choice_prob(ar_choice_unique_sorted < 0)); % prob(outcome>0), fraction of people borrowing fl_choice_prob_above_zero = sum(ar_choice_prob(ar_choice_unique_sorted > 0)); % prob(outcome=max(outcome)), fraction of people saving up to max of grid, % in principle if this is large, need to increase grid max value fl_choice_prob_max = sum(ar_choice_prob(ar_choice_unique_sorted == max(ar_choice_unique_sorted)));
f(y), f(c), f(a): Compute Distributional Statistics for outcomes
Compute these outcomes:
- percentiles:
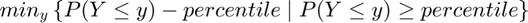
- share of outcome (consumption/assets) held by households below this percentile:
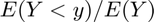 . Note that this statistics could exceed 1. Suppose the average level is negative, but there are both positive and negative
. Note that this statistics could exceed 1. Suppose the average level is negative, but there are both positive and negative 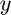 , then the statistics will first be what fraction of overall debt is held by up to this percentile, then it will exceed 100 percent, as we move towards the final
, then the statistics will first be what fraction of overall debt is held by up to this percentile, then it will exceed 100 percent, as we move towards the final 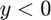 values, then as it goes through the
values, then as it goes through the  values, we will move back to 100 percent.
values, we will move back to 100 percent.
% cumulative share of total outcome held by up to this level for outcomes % like fraction of asset held by lowest highest fractions: E(X<x) ar_choice_unique_cumufrac = cumsum(ar_choice_prob.*ar_choice_unique_sorted)/fl_choice_mean; % Key Percentile Statistics ar_choice_prob_cumsum = cumsum(ar_choice_prob)*100; % ar_choice_percentiles: percentiles for the outcome variable ar_choice_percentiles = zeros(size(ar_fl_percentiles)); % fraction of aggregate outcome variable held up to this percentile ar_choice_perc_fracheld = zeros(size(ar_fl_percentiles)); for it_percentile = 1:length(ar_fl_percentiles) % get percentile of interest fl_cur_percentile = ar_fl_percentiles(it_percentile); % in the cumu prob array, first element higher or equal to current % percentile it_first_higher_idx = (cumsum(ar_choice_prob_cumsum >= fl_cur_percentile) == 1); % assign percentile fl_percentile = ar_choice_unique_sorted(it_first_higher_idx); fl_cumfrac = ar_choice_unique_cumufrac(it_first_higher_idx); if (length(fl_percentile) > 1) fl_percentile = fl_percentile(1); fl_cumfrac = fl_cumfrac(1); end ar_choice_percentiles(it_percentile) = fl_percentile; % asset held by up to this percentile ar_choice_perc_fracheld(it_percentile) = fl_cumfrac; end
Collect Statistics
ds_stats_map = containers.Map('KeyType','char', 'ValueType','any'); % scalar statistics ds_stats_map('fl_choice_mean') = fl_choice_mean; ds_stats_map('fl_choice_sd') = fl_choice_sd; ds_stats_map('fl_choice_coefofvar') = fl_choice_coefofvar; ds_stats_map('fl_choice_min') = fl_choice_min; ds_stats_map('fl_choice_max') = fl_choice_max; ds_stats_map('fl_choice_prob_zero') = fl_choice_prob_zero; ds_stats_map('fl_choice_prob_below_zero') = fl_choice_prob_below_zero; ds_stats_map('fl_choice_prob_above_zero') = fl_choice_prob_above_zero; ds_stats_map('fl_choice_prob_min') = fl_choice_prob_min; ds_stats_map('fl_choice_prob_max') = fl_choice_prob_max; % distributional array stats ds_stats_map('ar_fl_percentiles') = ar_fl_percentiles; ds_stats_map('ar_choice_percentiles') = ar_choice_percentiles; ds_stats_map('ar_choice_perc_fracheld') = ar_choice_perc_fracheld;
Display
if (bl_display_drvstats) disp('----------------------------------------'); disp('xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx'); disp(['Summary Statistics for: ' char(st_var_name)]) disp('xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx'); disp('----------------------------------------'); disp('fl_choice_mean'); disp(fl_choice_mean); disp('fl_choice_sd'); disp(fl_choice_sd); disp('fl_choice_coefofvar'); disp(fl_choice_coefofvar); disp('fl_choice_prob_zero'); disp(fl_choice_prob_zero); disp('fl_choice_prob_below_zero'); disp(fl_choice_prob_below_zero); disp('fl_choice_prob_above_zero'); disp(fl_choice_prob_above_zero); disp('fl_choice_prob_max'); disp(fl_choice_prob_max); disp('tb_disc_cumu'); tb_disc_cumu = table(ar_choice_unique_sorted', ar_choice_prob', ... ar_choice_prob_cumsum', ar_choice_unique_cumufrac'); st_var_name = [char(st_var_name) ' discrete val']; st_var_name_p = [char(st_var_name) ' prob mass']; tb_disc_cumu.Properties.VariableNames = ... matlab.lang.makeValidName([st_var_name, st_var_name_p, "CDF", "cumsum frac"]); disp(head(tb_disc_cumu,10)); disp(tail(tb_disc_cumu,10)); disp('tb_prob_drv'); tb_prob_drv = table(ar_fl_percentiles', ar_choice_percentiles', ar_choice_perc_fracheld'); st_var_name = [char(st_var_name) ' percentile values']; tb_prob_drv.Properties.VariableNames = matlab.lang.makeValidName(["percentiles", st_var_name, "frac of sum held below this percentile"]); disp(tb_prob_drv); % fft_container_map_display(ds_stats_map) end
----------------------------------------
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
Summary Statistics for: binom
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
----------------------------------------
fl_choice_mean
-1.0000
fl_choice_sd
2.5100
fl_choice_coefofvar
-2.5100
fl_choice_prob_zero
0.1416
fl_choice_prob_below_zero
0.5888
fl_choice_prob_above_zero
0.2696
fl_choice_prob_max
2.0589e-16
tb_disc_cumu
binomDiscreteVal binomDiscreteValProbMass CDF cumsumFrac
________________ ________________________ _________ __________
-10 2.2539e-05 0.0022539 0.00022539
-9 0.00028979 0.031233 0.0028335
-8 0.0018008 0.21132 0.01724
-7 0.0072034 0.93166 0.067664
-6 0.020838 3.0155 0.19269
-5 0.04644 7.6595 0.42489
-4 0.082928 15.952 0.75661
-3 0.12185 28.138 1.1222
-2 0.15014 43.152 1.4224
-1 0.15729 58.881 1.5797
binomDiscreteVal binomDiscreteValProbMass CDF cumsumFrac
________________ ________________________ ___ __________
11 6.0392e-06 100 1
12 1.0588e-06 100 1
13 1.5784e-07 100 1
14 1.973e-08 100 1
15 2.0293e-09 100 1
16 1.6725e-10 100 1
17 1.0619e-11 100 1
18 4.8762e-13 100 1
19 1.4412e-14 100 1
20 2.0589e-16 100 1
tb_prob_drv
percentiles binomDiscreteValPercentileValues fracOfSumHeldBelowThisPercentile
___________ ________________________________ ________________________________
0.1 -8 0.01724
1 -6 0.19269
5 -5 0.42489
10 -4 0.75661
15 -4 0.75661
20 -3 1.1222
25 -3 1.1222
35 -2 1.4224
50 -1 1.5797
65 0 1.5797
75 1 1.4694
80 1 1.4694
85 2 1.3197
90 2 1.3197
95 3 1.1865
99 5 1.0412
99.9 7 1.0052
end
ans =
Map with properties:
Count: 13
KeyType: char
ValueType: any