Solve One Asset Dynamic Programming Problem (Vectorized)
back to Fan's Dynamic Assets Repository Table of Content.
Contents
function result_map = ff_az_vf_vec(varargin)
FF_AZ_VF_VEC solve infinite horizon exo shock + endo asset problem
This program solves the infinite horizon dynamic single asset and single shock problem with vectorized codes. ff_az_vf shows looped codes. The solution is the same.
The vectorization takes advantage of implicit parallization that modern computers have when same instructions are given for different blocks of data With vectorization, we face a tradeoff between memory and speed. Suppose we have many shock points and many states points, if we build all states and choices into one single matrix and compute consumption, utility, etc over that entire matrix, that might be more efficient than computing consumption, utility, etc by subset of that matrix over a loop, but there is time required for generating that large input matrix, and if there are too many states, a computer could run out of memory.
The design philosophy here is that we vectorize the endogenous states and choices into matrixes, but do not include the exogeous states (shocks). The exogenous shocks remain looped. This means we can potentially have multiple shock variables discretized over a large number of shock states, and the computer would not run into memory problems. The speed gain from vectoring the rest of the problem conditional on shocks is very large compared to the pure looped version of the problem. Even if more memory is available, including the exogenous states in the vectorization process might not be speed improving.
Note one key issue is whether a programming language is row or column major depending on which, states should be rows or columns.
Another programming issue is the idea of broadcasting vs matrix algebra, both are used here. Since Matlab R2016b, matrix broadcasting has been allowed, which means the sum of a N by 1 and 1 by M is N by M. This is unrelated to matrix algebra. Matrix array broadcasting is very useful because it reduces the dimensionality of our model input state and choice and shock vectors, offering greater code clarity.
@param param_map container parameter container
@param support_map container support container
@param armt_map container container with states, choices and shocks grids that are inputs for grid based solution algorithm
@param func_map container container with function handles for consumption cash-on-hand etc.
@return result_map container contains policy function matrix, value function matrix, iteration results, and policy function, value function and iteration results tables.
keys included in result_map:
- mt_val matrix states_n by shock_n matrix of converged value function grid
- mt_pol_a matrix states_n by shock_n matrix of converged policy function grid
- ar_val_diff_norm array if bl_post = true it_iter_last by 1 val function difference between iteration
- ar_pol_diff_norm array if bl_post = true it_iter_last by 1 policy function difference between iterations
- mt_pol_perc_change matrix if bl_post = true it_iter_last by shock_n the proportion of grid points at which policy function changed between current and last iteration for each element of shock
@example
% Get Default Parameters
it_param_set = 2;
[param_map, support_map] = ffs_abz_set_default_param(it_param_set);
% Change Keys in param_map
param_map('it_a_n') = 500;
param_map('it_z_n') = 11;
param_map('fl_a_max') = 100;
param_map('fl_w') = 1.3;
% Change Keys support_map
support_map('bl_display') = false;
support_map('bl_post') = true;
support_map('bl_display_final') = false;
% Call Program with external parameters that override defaults.
ff_az_vf_vec(param_map, support_map);@include
@seealso
- save loop: ff_az_vf
- save vectorized: ff_az_vf_vec
- save optimized-vectorized: ff_az_vf_vecsv
- save + borr loop: ff_abz_vf
- save + borr vectorized: ff_abz_vf_vec
- save + borr optimized-vectorized: ff_abz_vf_vecsv
Default
- it_param_set = 1: quick test
- it_param_set = 2: benchmark run
- it_param_set = 3: benchmark profile
- it_param_set = 4: press publish button
it_param_set = 4; bl_input_override = true; [param_map, support_map] = ffs_az_set_default_param(it_param_set); % Note: param_map and support_map can be adjusted here or outside to override defaults % param_map('it_a_n') = 750; % param_map('it_z_n') = 15; [armt_map, func_map] = ffs_az_get_funcgrid(param_map, support_map, bl_input_override); % 1 for override default_params = {param_map support_map armt_map func_map};
Parse Parameters 1
% if varargin only has param_map and support_map, params_len = length(varargin); [default_params{1:params_len}] = varargin{:}; param_map = [param_map; default_params{1}]; support_map = [support_map; default_params{2}]; if params_len >= 1 && params_len <= 2 % If override param_map, re-generate armt and func if they are not % provided bl_input_override = true; [armt_map, func_map] = ffs_az_get_funcgrid(param_map, support_map, bl_input_override); else % Override all armt_map = [armt_map; default_params{3}]; func_map = [func_map; default_params{4}]; end % append function name st_func_name = 'ff_az_vf_vec'; support_map('st_profile_name_main') = [st_func_name support_map('st_profile_name_main')]; support_map('st_mat_name_main') = [st_func_name support_map('st_mat_name_main')]; support_map('st_img_name_main') = [st_func_name support_map('st_img_name_main')];
Parse Parameters 2
% armt_map params_group = values(armt_map, {'ar_a', 'mt_z_trans', 'ar_z'}); [ar_a, mt_z_trans, ar_z] = params_group{:}; % func_map params_group = values(func_map, {'f_util_log', 'f_util_crra', 'f_cons', 'f_coh'}); [f_util_log, f_util_crra, f_cons, f_coh] = params_group{:}; % param_map params_group = values(param_map, {'it_a_n', 'it_z_n', 'fl_crra', 'fl_beta', 'fl_nan_replace'}); [it_a_n, it_z_n, fl_crra, fl_beta, fl_nan_replace] = params_group{:}; params_group = values(param_map, {'it_maxiter_val', 'fl_tol_val', 'fl_tol_pol', 'it_tol_pol_nochange'}); [it_maxiter_val, fl_tol_val, fl_tol_pol, it_tol_pol_nochange] = params_group{:}; % support_map params_group = values(support_map, {'bl_profile', 'st_profile_path', ... 'st_profile_prefix', 'st_profile_name_main', 'st_profile_suffix',... 'bl_time', 'bl_display', 'it_display_every', 'bl_post'}); [bl_profile, st_profile_path, ... st_profile_prefix, st_profile_name_main, st_profile_suffix, ... bl_time, bl_display, it_display_every, bl_post] = params_group{:};
Initialize Output Matrixes
include mt_pol_idx which we did not have in looped code
mt_val_cur = zeros(length(ar_a),length(ar_z)); mt_val = mt_val_cur - 1; mt_pol_a = zeros(length(ar_a),length(ar_z)); mt_pol_a_cur = mt_pol_a - 1; mt_pol_idx = zeros(length(ar_a),length(ar_z));
Initialize Convergence Conditions
bl_vfi_continue = true; it_iter = 0; ar_val_diff_norm = zeros([it_maxiter_val, 1]); ar_pol_diff_norm = zeros([it_maxiter_val, 1]); mt_pol_perc_change = zeros([it_maxiter_val, it_z_n]);
Iterate Value Function
Loop solution with 4 nested loops
- loop 1: over exogenous states
- loop 2: over endogenous states
- loop 3: over choices
- loop 4: add future utility, integration--loop over future shocks
% Start Profile if (bl_profile) close all; profile off; profile on; end % Start Timer if (bl_time) tic; end % Value Function Iteration while bl_vfi_continue
it_iter = it_iter + 1;
Solve Optimization Problem Current Iteration
Only this segment of code differs between ff_az_vf and ff_az_vf_vec
% loop 1: over exogenous states % incorporating these shocks into vectorization has high memory burden % but insignificant speed gains. Keeping this loop allows for large % number of shocks without overwhelming memory for it_z_i = 1:length(ar_z) % Current Shock fl_z = ar_z(it_z_i); % Consumption: fl_z = 1 by 1, ar_a = 1 by N, ar_a' = N by 1 % mt_c is N by N: matrix broadcasting, expand to matrix from arrays mt_c = f_cons(fl_z, ar_a, ar_a'); % EVAL current utility: N by N, f_util defined earlier if (fl_crra == 1) mt_utility = f_util_log(mt_c); else mt_utility = f_util_crra(mt_c); end % f(z'|z), 1 by Z ar_z_trans_condi = mt_z_trans(it_z_i,:); % EVAL EV((A',K'),Z'|Z) = V((A',K'),Z') x p(z'|z)', (N by Z) x (Z by 1) = N by 1 % Note: transpose ar_z_trans_condi from 1 by Z to Z by 1 % Note: matrix multiply not dot multiply mt_evzp_condi_z = mt_val_cur * ar_z_trans_condi'; % EVAL add on future utility, N by N + N by 1, broadcast again mt_utility = mt_utility + fl_beta*mt_evzp_condi_z; mt_utility(mt_c <= 0) = fl_nan_replace; % Optimization: remember matlab is column major, rows must be % choices, columns must be states % <https://en.wikipedia.org/wiki/Row-_and_column-major_order COLUMN-MAJOR> % mt_utility is N by N, rows are choices, cols are states. [ar_opti_val1_z, ar_opti_idx_z] = max(mt_utility); mt_val(:,it_z_i) = ar_opti_val1_z; mt_pol_a(:,it_z_i) = ar_a(ar_opti_idx_z); if (it_iter == (it_maxiter_val + 1)) mt_pol_idx(:,it_z_i) = ar_opti_idx_z; end end
Check Tolerance and Continuation
% Difference across iterations ar_val_diff_norm(it_iter) = norm(mt_val - mt_val_cur); ar_pol_diff_norm(it_iter) = norm(mt_pol_a - mt_pol_a_cur); mt_pol_perc_change(it_iter, :) = sum((mt_pol_a ~= mt_pol_a_cur))/(it_a_n); % Update mt_val_cur = mt_val; mt_pol_a_cur = mt_pol_a; % Print Iteration Results if (bl_display && (rem(it_iter, it_display_every)==0)) fprintf('VAL it_iter:%d, fl_diff:%d, fl_diff_pol:%d\n', ... it_iter, ar_val_diff_norm(it_iter), ar_pol_diff_norm(it_iter)); tb_valpol_iter = array2table([mean(mt_val_cur,1); mean(mt_pol_a_cur,1); ... mt_val_cur(it_a_n,:); mt_pol_a_cur(it_a_n,:)]); tb_valpol_iter.Properties.VariableNames = strcat('z', string((1:size(mt_val_cur,2)))); tb_valpol_iter.Properties.RowNames = {'mval', 'map', 'Hval', 'Hap'}; disp('mval = mean(mt_val_cur,1), average value over a') disp('map = mean(mt_pol_a_cur,1), average choice over a') disp('Hval = mt_val_cur(it_a_n,:), highest a state val') disp('Hap = mt_pol_a_cur(it_a_n,:), highest a state choice') disp(tb_valpol_iter); end % Continuation Conditions: % 1. if value function convergence criteria reached % 2. if policy function variation over iterations is less than % threshold if (it_iter == (it_maxiter_val + 1)) bl_vfi_continue = false; elseif ((it_iter == it_maxiter_val) || ... (ar_val_diff_norm(it_iter) < fl_tol_val) || ... (sum(ar_pol_diff_norm(max(1, it_iter-it_tol_pol_nochange):it_iter)) < fl_tol_pol)) % Fix to max, run again to save results if needed it_iter_last = it_iter; it_iter = it_maxiter_val; end
end % End Timer if (bl_time) toc; end % End Profile if (bl_profile) profile off profile viewer st_file_name = [st_profile_prefix st_profile_name_main st_profile_suffix]; profsave(profile('info'), strcat(st_profile_path, st_file_name)); end
Process Optimal Choices
for choices outcomes, store as cell with two elements, first element is the y(a,z), outcome given states, the second element will be solved found in ff_ds_vf and other distributions files. It stores what are the probability mass function of y, along with sorted unique values of y.
result_map = containers.Map('KeyType','char', 'ValueType','any'); result_map('mt_val') = mt_val; result_map('mt_pol_idx') = mt_pol_idx; result_map('cl_mt_pol_a') = {mt_pol_a, zeros(1)}; result_map('cl_mt_coh') = {f_coh(ar_z, ar_a'), zeros(1)}; result_map('cl_mt_pol_c') = {f_coh(ar_z, ar_a') - mt_pol_a, zeros(1)}; result_map('ar_st_pol_names') = ["mt_val", "cl_mt_pol_a", "cl_mt_coh", "cl_mt_pol_c"]; if (bl_post) bl_input_override = true; result_map('ar_val_diff_norm') = ar_val_diff_norm(1:it_iter_last); result_map('ar_pol_diff_norm') = ar_pol_diff_norm(1:it_iter_last); result_map('mt_pol_perc_change') = mt_pol_perc_change(1:it_iter_last, :); result_map = ff_az_vf_post(param_map, support_map, armt_map, func_map, result_map, bl_input_override); end
valgap = norm(mt_val - mt_val_cur): value function difference across iterations
polgap = norm(mt_pol_a - mt_pol_a_cur): policy function difference across iterations
z1 = z1 perc change: sum((mt_pol_a ~= mt_pol_a_cur))/(it_a_n): percentage of state space points conditional on shock where the policy function is changing across iterations
valgap polgap z1_0_34741 z2_0_40076 z3_0_4623 z4_0_5333 z5_0_61519 z6_0_70966 z10_1_2567 z11_1_4496 z12_1_6723 z13_1_9291 z14_2_2253 z15_2_567
________ ________ __________ __________ _________ _________ __________ __________ __________ __________ __________ __________ __________ _________
iter=1 163.75 106.07 1 1 1 1 1 1 1 1 1 1 1 1
iter=2 124.31 1532.9 0.996 0.996 0.996 0.996 0.99733 0.99733 1 1 1 1 1 1
iter=3 102.03 510.84 0.988 0.99067 0.99067 0.99067 0.99333 0.992 0.99733 1 1 1 1 1
iter=4 86.034 255.3 0.98 0.98 0.98133 0.98267 0.984 0.984 0.99867 0.99867 1 1 1 1
iter=5 73.685 152.77 0.96667 0.97067 0.96933 0.972 0.97467 0.97467 0.992 0.996 0.99867 1 1 1
iter=6 63.774 101.47 0.95333 0.95467 0.95733 0.95867 0.96267 0.96533 0.98533 0.99067 0.996 1 1 1
iter=7 55.621 72.103 0.936 0.94 0.944 0.94667 0.94667 0.95333 0.97467 0.98133 0.992 0.99733 1 1
iter=8 48.798 53.69 0.92 0.92133 0.924 0.92933 0.93467 0.93867 0.96533 0.97467 0.98267 0.98933 0.996 1
iter=9 43.012 41.353 0.9 0.90133 0.90533 0.90933 0.916 0.92133 0.95467 0.96533 0.97467 0.984 0.992 0.99467
iter=10 38.059 32.75 0.87333 0.87867 0.88533 0.89067 0.89867 0.9 0.93733 0.94933 0.95867 0.96933 0.98267 0.99333
iter=11 33.783 26.505 0.85467 0.856 0.86133 0.86533 0.87733 0.88533 0.92533 0.93467 0.94667 0.95733 0.97067 0.98267
iter=12 30.068 21.79 0.82267 0.83067 0.83333 0.844 0.84933 0.85867 0.89333 0.912 0.92533 0.94667 0.95867 0.96667
iter=13 26.824 18.165 0.80133 0.80533 0.80933 0.82267 0.82667 0.83333 0.88 0.89333 0.90933 0.91467 0.93067 0.952
iter=14 23.979 15.333 0.77333 0.77867 0.784 0.78533 0.79467 0.80667 0.84933 0.868 0.884 0.89867 0.916 0.92933
iter=15 21.472 13.055 0.73333 0.73733 0.74933 0.76133 0.76533 0.78133 0.82667 0.83867 0.852 0.876 0.89333 0.912
iter=16 19.259 11.195 0.70667 0.70933 0.72133 0.72933 0.73867 0.744 0.79733 0.808 0.82667 0.844 0.86133 0.884
iter=17 17.297 9.6488 0.67067 0.67467 0.67733 0.68933 0.69733 0.71067 0.76533 0.78 0.796 0.81467 0.83067 0.852
iter=18 15.555 8.4101 0.63067 0.63333 0.652 0.65733 0.66933 0.67333 0.72667 0.744 0.76 0.78267 0.79867 0.82267
iter=19 14.006 7.3437 0.58667 0.60533 0.60533 0.61467 0.628 0.63467 0.68933 0.704 0.72933 0.748 0.76667 0.78267
iter=20 12.624 6.449 0.54933 0.55333 0.56533 0.576 0.588 0.596 0.65467 0.668 0.688 0.69867 0.732 0.74667
iter=21 11.39 5.6505 0.5 0.50933 0.52 0.53067 0.54 0.54533 0.60133 0.62533 0.63733 0.66533 0.68267 0.70533
iter=22 10.287 5.0083 0.46267 0.46533 0.47467 0.47733 0.49067 0.50933 0.56267 0.57467 0.59333 0.61867 0.63733 0.66667
iter=23 9.3002 4.4887 0.40533 0.42 0.41867 0.436 0.44933 0.45867 0.508 0.53067 0.552 0.57467 0.59467 0.61333
iter=24 8.4155 4.0328 0.356 0.36 0.37733 0.37733 0.38933 0.40267 0.45867 0.476 0.49867 0.516 0.544 0.56267
iter=25 7.6221 3.5934 0.31333 0.312 0.32667 0.33467 0.34133 0.356 0.41333 0.42533 0.44667 0.46667 0.484 0.516
iter=26 6.91 3.2085 0.272 0.27867 0.28133 0.30133 0.304 0.30933 0.356 0.37467 0.388 0.41067 0.428 0.452
iter=27 6.2702 2.8585 0.236 0.24933 0.24667 0.248 0.26133 0.272 0.31867 0.33333 0.34533 0.364 0.384 0.40267
iter=28 5.6953 2.5765 0.21467 0.21467 0.22133 0.228 0.24133 0.244 0.27867 0.296 0.30667 0.31867 0.34133 0.35867
iter=29 5.1782 2.306 0.184 0.188 0.20133 0.20267 0.20267 0.212 0.24667 0.256 0.27333 0.29467 0.30267 0.32133
iter=30 4.7129 2.0418 0.16 0.164 0.16267 0.17333 0.18133 0.18133 0.22267 0.228 0.24133 0.25333 0.264 0.288
iter=31 4.2941 1.8115 0.14133 0.14933 0.156 0.156 0.16267 0.17067 0.19067 0.2 0.21067 0.21733 0.24267 0.24533
iter=32 3.9168 1.6523 0.12933 0.128 0.12933 0.13333 0.13467 0.13867 0.17467 0.18267 0.192 0.2 0.20267 0.22533
iter=33 3.5768 1.5041 0.108 0.112 0.112 0.11467 0.124 0.12667 0.14533 0.156 0.16 0.17733 0.192 0.19867
iter=34 3.2703 1.4169 0.089333 0.093333 0.10667 0.10933 0.10933 0.116 0.136 0.13467 0.152 0.15467 0.16 0.176
iter=35 2.9938 1.3063 0.085333 0.081333 0.08 0.096 0.093333 0.092 0.116 0.12533 0.128 0.136 0.14533 0.15333
iter=36 2.7442 1.2085 0.073333 0.078667 0.073333 0.073333 0.08 0.082667 0.10133 0.108 0.11467 0.11867 0.13333 0.13467
iter=37 2.5187 1.1046 0.058667 0.066667 0.066667 0.066667 0.072 0.073333 0.086667 0.093333 0.1 0.10667 0.108 0.12267
iter=38 2.3149 0.9803 0.053333 0.050667 0.062667 0.058667 0.061333 0.066667 0.08 0.084 0.090667 0.1 0.098667 0.11067
iter=39 2.1305 0.77536 0.044 0.045333 0.046667 0.053333 0.056 0.053333 0.065333 0.074667 0.072 0.074667 0.088 0.085333
iter=40 1.9634 0.74607 0.041333 0.042667 0.037333 0.042667 0.041333 0.044 0.057333 0.06 0.064 0.069333 0.08 0.078667
iter=41 1.8119 0.714 0.04 0.032 0.034667 0.041333 0.038667 0.046667 0.052 0.053333 0.06 0.064 0.061333 0.073333
iter=42 1.6744 0.61466 0.025333 0.034667 0.034667 0.028 0.034667 0.030667 0.042667 0.045333 0.048 0.056 0.057333 0.062667
iter=43 1.5494 0.57239 0.024 0.028 0.026667 0.028 0.030667 0.033333 0.038667 0.04 0.050667 0.046667 0.052 0.056
iter=44 1.4355 0.51494 0.016 0.022667 0.022667 0.022667 0.025333 0.028 0.034667 0.036 0.036 0.042667 0.042667 0.044
iter=45 1.3316 0.50433 0.016 0.018667 0.02 0.021333 0.02 0.025333 0.025333 0.029333 0.024 0.032 0.041333 0.04
iter=46 1.2367 0.40288 0.018667 0.013333 0.017333 0.017333 0.02 0.017333 0.028 0.022667 0.028 0.029333 0.026667 0.038667
iter=47 1.1498 0.38952 0.014667 0.0093333 0.013333 0.016 0.016 0.013333 0.02 0.028 0.024 0.025333 0.033333 0.025333
iter=48 1.0701 0.33652 0.010667 0.012 0.014667 0.013333 0.018667 0.010667 0.016 0.018667 0.021333 0.021333 0.02 0.029333
iter=49 0.99696 0.28366 0.004 0.0093333 0.008 0.0066667 0.0053333 0.012 0.012 0.012 0.016 0.016 0.02 0.018667
iter=50 0.92962 0.29039 0.010667 0.008 0.008 0.010667 0.008 0.008 0.010667 0.017333 0.013333 0.016 0.016 0.024
iter=56 0.62025 0.22154 0.004 0.0013333 0.0013333 0.0026667 0.0013333 0.0026667 0.004 0.0026667 0.010667 0.0066667 0.0066667 0.0066667
iter=57 0.58092 0.14927 0.0013333 0.0026667 0.004 0 0.0026667 0.0026667 0.0053333 0.0066667 0 0.004 0.0053333 0.004
iter=58 0.5443 0.16352 0.0026667 0.0013333 0.0013333 0.0013333 0.004 0 0.0026667 0.0013333 0.0026667 0.0053333 0.008 0.004
iter=59 0.51018 0.13847 0 0 0.0013333 0.0026667 0.004 0.0026667 0.0013333 0.0026667 0.004 0.0026667 0.0026667 0.0013333
iter=60 0.47836 0.14346 0.0013333 0 0.004 0.0013333 0 0.0013333 0.004 0.0013333 0.0026667 0.004 0.0013333 0.0053333
iter=61 0.44865 0.13351 0.0013333 0.0053333 0 0.0013333 0.0013333 0.0026667 0.0013333 0.0013333 0.004 0.0026667 0 0.0053333
iter=62 0.42089 0.13847 0.0013333 0.0026667 0 0.0013333 0 0 0.0026667 0.0013333 0 0.0053333 0.0026667 0
iter=63 0.39494 0.11562 0 0 0 0.0013333 0 0.0013333 0 0.0026667 0.0026667 0 0.0026667 0.0013333
iter=64 0.37067 0.066756 0.0013333 0 0 0.0013333 0 0.0013333 0.0013333 0 0.0013333 0.0013333 0.0013333 0.0013333
iter=65 0.34796 0.094407 0 0 0.0026667 0.0026667 0 0 0 0.0013333 0 0 0 0.0013333
iter=66 0.32668 0.094407 0 0 0 0 0 0 0 0.0026667 0.0013333 0 0.0013333 0.0013333
iter=67 0.30676 0.066756 0 0 0.0013333 0 0 0.0013333 0.0013333 0 0 0 0 0
iter=68 0.28808 0.066756 0 0 0 0.0013333 0.0013333 0 0 0 0.0013333 0 0.0013333 0.0013333
iter=69 0.27057 0.066756 0 0 0 0 0.0013333 0 0.0013333 0 0 0.0013333 0.0013333 0
iter=70 0.25415 0.066756 0 0 0 0 0 0 0.0013333 0 0 0 0 0
iter=71 0.23875 0.066756 0 0 0 0 0 0 0 0 0.0013333 0 0 0.0013333
iter=72 0.22429 0.066756 0 0 0 0 0 0 0.0013333 0 0 0 0 0
iter=73 0.21073 0.066756 0 0 0 0.0013333 0 0 0 0 0 0 0.0013333 0
iter=74 0.198 0.066756 0 0 0 0 0 0.0013333 0 0.0013333 0 0 0 0.0013333
iter=75 0.18605 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=76 0.17483 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=77 0.16429 0.066756 0 0 0 0 0 0 0 0 0 0.0013333 0 0
iter=78 0.15439 0.066756 0 0 0 0 0 0 0 0 0 0.0013333 0 0
iter=79 0.14509 0.066756 0 0 0 0 0 0 0 0 0 0 0.0013333 0
iter=80 0.13636 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=81 0.12815 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=82 0.12044 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=83 0.1132 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=84 0.1064 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=85 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=86 0.093993 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=87 0.088346 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=88 0.083039 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=89 0.078052 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=90 0.073365 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=91 0.068959 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=92 0.064819 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=93 0.060927 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=94 0.05727 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=95 0.053832 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=96 0.050601 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=97 0.047563 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=98 0.044709 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=99 0.042025 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=100 0.039503 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=101 0.037133 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=102 0.034904 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=103 0.03281 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=104 0.030841 0 0 0 0 0 0 0 0 0 0 0 0 0
iter=105 0.02899 0 0 0 0 0 0 0 0 0 0 0 0 0
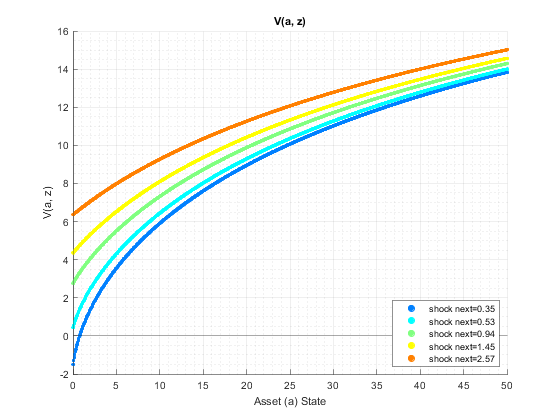
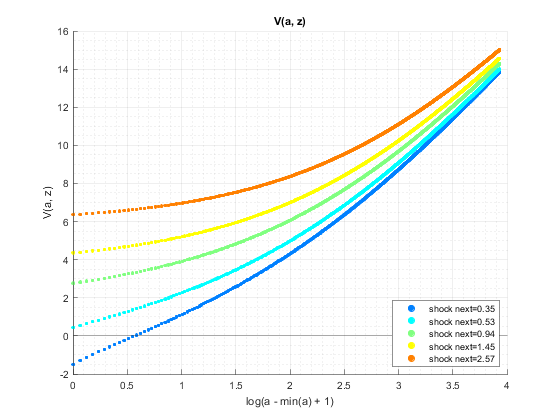
tb_val: V(a,z) value at each state space point
z1_0_34741 z2_0_40076 z3_0_4623 z4_0_5333 z5_0_61519 z6_0_70966 z10_1_2567 z11_1_4496 z12_1_6723 z13_1_9291 z14_2_2253 z15_2_567
__________ __________ _________ _________ __________ __________ __________ __________ __________ __________ __________ _________
a1=0 -1.496 -0.85738 -0.20677 0.4326 1.051 1.6461 3.834 4.3533 4.868 5.3788 5.8799 6.3576
a2=0.0667557 -1.2889 -0.68792 -0.068348 0.54551 1.143 1.721 3.8742 4.3894 4.9006 5.4083 5.9069 6.3825
a3=0.133511 -1.1195 -0.54598 0.050085 0.64396 1.2251 1.7912 3.9139 4.4251 4.933 5.4377 5.9338 6.4073
a4=0.200267 -0.96773 -0.41407 0.16308 0.74017 1.3064 1.8584 3.9533 4.4604 4.9651 5.4669 5.9606 6.4319
a5=0.267023 -0.82642 -0.29338 0.26557 0.82676 1.3813 1.924 3.9925 4.4955 4.997 5.4959 5.9872 6.4564
a6=0.333778 -0.69878 -0.18077 0.3638 0.91224 1.4539 1.9876 4.0313 4.5305 5.0287 5.5248 6.0136 6.4809
a7=0.400534 -0.57856 -0.074032 0.45817 0.99503 1.5263 2.0483 4.0696 4.5651 5.0602 5.5536 6.04 6.5052
a8=0.46729 -0.45992 0.029893 0.54774 1.0717 1.5944 2.1088 4.1075 4.5995 5.0915 5.5823 6.0663 6.5295
a9=0.534045 -0.35088 0.12737 0.63413 1.1482 1.6607 2.1681 4.1449 4.6335 5.1225 5.6108 6.0925 6.5537
a10=0.600801 -0.24733 0.22021 0.71739 1.2225 1.7257 2.226 4.1821 4.6674 5.1534 5.6391 6.1185 6.5778
a11=0.667557 -0.14534 0.31092 0.79796 1.2948 1.7903 2.2822 4.2189 4.701 5.1841 5.6672 6.1444 6.6018
a12=0.734312 -0.048003 0.39986 0.87689 1.3637 1.8524 2.3374 4.2554 4.7343 5.2145 5.6952 6.1702 6.6257
a13=0.801068 0.046006 0.48497 0.95338 1.4319 1.9133 2.3921 4.2916 4.7675 5.2448 5.7231 6.1959 6.6494
a14=0.867824 0.13615 0.56673 1.0277 1.4991 1.9727 2.4461 4.3278 4.8003 5.2749 5.7508 6.2214 6.6731
a15=0.934579 0.22501 0.64659 1.0996 1.5645 2.0312 2.499 4.3636 4.8329 5.3049 5.7783 6.2469 6.6967
a16=1.00134 0.3102 0.72515 1.1699 1.6285 2.0894 2.5509 4.3991 4.8653 5.3348 5.8057 6.2722 6.7201
a17=1.06809 0.3935 0.80188 1.24 1.6907 2.1461 2.6021 4.4343 4.8976 5.3644 5.8329 6.2974 6.7435
a18=1.13485 0.47421 0.87628 1.308 1.7519 2.2019 2.6524 4.4692 4.9297 5.3939 5.8601 6.3225 6.7668
a19=1.2016 0.55339 0.94865 1.3745 1.8127 2.2566 2.7021 4.5038 4.9615 5.4232 5.887 6.3475 6.79
a20=1.26836 0.63134 1.0195 1.4394 1.8723 2.3104 2.7515 4.5382 4.9931 5.4523 5.9139 6.3723 6.813
a21=1.33511 0.70675 1.0896 1.5027 1.9307 2.3634 2.8003 4.5722 5.0245 5.4813 5.9407 6.397 6.836
a22=1.40187 0.78048 1.1581 1.5655 1.9881 2.4162 2.8482 4.606 5.0558 5.5101 5.9674 6.4216 6.8589
a23=1.46862 0.85238 1.2252 1.6276 2.0443 2.468 2.8955 4.6396 5.0868 5.5387 5.9939 6.4462 6.8817
a24=1.53538 0.92293 1.291 1.6885 2.0996 2.5191 2.9422 4.673 5.1176 5.5672 6.0203 6.4706 6.9045
a25=1.60214 0.99302 1.3552 1.7481 2.1547 2.5695 2.9885 4.7063 5.1483 5.5956 6.0466 6.495 6.9271
a26=1.66889 1.0615 1.4184 1.8067 2.2091 2.6192 3.034 4.7393 5.1787 5.6237 6.0727 6.5193 6.9497
a27=1.73565 1.1286 1.4813 1.8643 2.2626 2.6682 3.0793 4.7722 5.209 5.6517 6.0987 6.5435 6.9723
a28=1.8024 1.1944 1.543 1.9208 2.3151 2.7166 3.1243 4.8048 5.2391 5.6797 6.1246 6.5675 6.9947
a29=1.86916 1.2588 1.6034 1.9772 2.3671 2.7646 3.1687 4.8371 5.2691 5.7075 6.1504 6.5915 7.017
a30=1.93591 1.3221 1.663 2.0328 2.4182 2.8122 3.2125 4.8693 5.2989 5.7351 6.176 6.6153 7.0393
a31=2.00267 1.3847 1.7215 2.0876 2.4686 2.8592 3.256 4.9013 5.3286 5.7626 6.2016 6.6391 7.0615
a32=2.06943 1.4466 1.779 2.1414 2.5185 2.9057 3.2989 4.933 5.3581 5.79 6.227 6.6628 7.0836
a33=2.13618 1.5075 1.8357 2.1946 2.5682 2.9515 3.3413 4.9645 5.3874 5.8173 6.2522 6.6863 7.1056
a34=2.20294 1.5674 1.8923 2.2469 2.6172 2.9969 3.3834 4.9958 5.4165 5.8444 6.2774 6.7098 7.1275
a35=2.26969 1.6263 1.9479 2.2986 2.6656 3.0417 3.4251 5.0269 5.4455 5.8714 6.3025 6.7332 7.1493
a36=2.33645 1.6844 2.0028 2.3496 2.7133 3.0861 3.4665 5.0578 5.4744 5.8982 6.3275 6.7565 7.1711
a37=2.4032 1.7414 2.0567 2.4003 2.7606 3.1301 3.5077 5.0886 5.5031 5.9249 6.3524 6.7796 7.1928
a38=2.46996 1.7977 2.1101 2.4506 2.8073 3.1738 3.5485 5.1193 5.5316 5.9515 6.3772 6.8027 7.2144
a39=2.53672 1.8538 2.1627 2.5002 2.8535 3.2171 3.5888 5.1499 5.56 5.9779 6.4019 6.8257 7.2359
a40=2.60347 1.909 2.2145 2.5491 2.899 3.26 3.6288 5.1802 5.5882 6.0043 6.4265 6.8486 7.2573
a41=2.67023 1.9635 2.2657 2.5974 2.9444 3.3025 3.6685 5.2103 5.6163 6.0305 6.451 6.8714 7.2787
a42=2.73698 2.0173 2.3167 2.6452 2.9895 3.3445 3.7077 5.2403 5.6442 6.0565 6.4753 6.8942 7.3
a43=2.80374 2.0703 2.3672 2.6925 3.034 3.3861 3.7466 5.2701 5.672 6.0825 6.4996 6.9169 7.3212
a44=2.87049 2.1228 2.4171 2.7392 3.0781 3.4273 3.7853 5.2997 5.6997 6.1084 6.5238 6.9395 7.3423
a45=2.93725 2.1745 2.4663 2.7854 3.1217 3.4682 3.8236 5.3292 5.7273 6.1342 6.5478 6.962 7.3635
a46=3.00401 2.2255 2.5149 2.8315 3.1649 3.5088 3.8616 5.3585 5.7548 6.1598 6.5718 6.9845 7.3845
a47=3.07076 2.2762 2.563 2.8771 3.2077 3.5489 3.8994 5.3876 5.7821 6.1854 6.5957 7.0068 7.4055
a48=3.13752 2.3265 2.6105 2.9222 3.2501 3.5889 3.937 5.4166 5.8092 6.2108 6.6194 7.029 7.4264
a49=3.20427 2.3762 2.6576 2.9669 3.2921 3.6286 3.9744 5.4454 5.8362 6.2361 6.6431 7.0512 7.4472
a50=3.27103 2.4254 2.7041 3.0111 3.3337 3.668 4.0114 5.474 5.8631 6.2613 6.6666 7.0733 7.4679
a701=46.729 13.458 13.509 13.568 13.632 13.7 13.774 14.124 14.227 14.338 14.455 14.577 14.7
a702=46.7957 13.466 13.517 13.576 13.639 13.708 13.782 14.131 14.234 14.345 14.462 14.584 14.707
a703=46.8625 13.474 13.525 13.584 13.647 13.716 13.789 14.138 14.241 14.351 14.468 14.59 14.713
a704=46.9292 13.482 13.533 13.591 13.655 13.724 13.797 14.145 14.248 14.358 14.475 14.597 14.72
a705=46.996 13.49 13.541 13.599 13.663 13.731 13.805 14.153 14.255 14.365 14.482 14.604 14.726
a706=47.0628 13.498 13.549 13.607 13.671 13.739 13.812 14.16 14.263 14.372 14.489 14.61 14.733
a707=47.1295 13.506 13.557 13.615 13.678 13.747 13.82 14.167 14.27 14.379 14.496 14.617 14.739
a708=47.1963 13.514 13.565 13.623 13.686 13.754 13.827 14.174 14.277 14.386 14.502 14.624 14.746
a709=47.263 13.522 13.573 13.631 13.694 13.762 13.835 14.181 14.284 14.393 14.509 14.63 14.752
a710=47.3298 13.53 13.581 13.638 13.702 13.77 13.842 14.188 14.291 14.4 14.516 14.637 14.759
a711=47.3965 13.537 13.588 13.646 13.709 13.777 13.85 14.196 14.298 14.407 14.523 14.643 14.765
a712=47.4633 13.545 13.596 13.654 13.717 13.785 13.858 14.203 14.305 14.414 14.529 14.65 14.771
a713=47.53 13.553 13.604 13.662 13.725 13.793 13.865 14.21 14.312 14.42 14.536 14.657 14.778
a714=47.5968 13.561 13.612 13.67 13.732 13.8 13.873 14.217 14.319 14.427 14.543 14.663 14.784
a715=47.6636 13.569 13.62 13.677 13.74 13.808 13.88 14.224 14.326 14.434 14.549 14.67 14.791
a716=47.7303 13.577 13.628 13.685 13.748 13.815 13.888 14.231 14.333 14.441 14.556 14.676 14.797
a717=47.7971 13.585 13.636 13.693 13.756 13.823 13.895 14.238 14.34 14.448 14.563 14.683 14.804
a718=47.8638 13.593 13.643 13.701 13.763 13.83 13.903 14.245 14.346 14.455 14.57 14.689 14.81
a719=47.9306 13.601 13.651 13.708 13.771 13.838 13.91 14.252 14.353 14.461 14.576 14.696 14.817
a720=47.9973 13.609 13.659 13.716 13.778 13.846 13.917 14.259 14.36 14.468 14.583 14.703 14.823
a721=48.0641 13.616 13.667 13.724 13.786 13.853 13.925 14.266 14.367 14.475 14.59 14.709 14.829
a722=48.1308 13.624 13.674 13.731 13.794 13.861 13.932 14.273 14.374 14.482 14.596 14.716 14.836
a723=48.1976 13.632 13.682 13.739 13.801 13.868 13.94 14.28 14.381 14.489 14.603 14.722 14.842
a724=48.2644 13.64 13.69 13.747 13.809 13.876 13.947 14.287 14.388 14.495 14.61 14.729 14.848
a725=48.3311 13.648 13.698 13.754 13.816 13.883 13.955 14.294 14.395 14.502 14.616 14.735 14.855
a726=48.3979 13.655 13.705 13.762 13.824 13.891 13.962 14.301 14.402 14.509 14.623 14.742 14.861
a727=48.4646 13.663 13.713 13.77 13.832 13.898 13.969 14.308 14.409 14.516 14.629 14.748 14.868
a728=48.5314 13.671 13.721 13.777 13.839 13.906 13.977 14.315 14.415 14.522 14.636 14.755 14.874
a729=48.5981 13.679 13.729 13.785 13.847 13.913 13.984 14.322 14.422 14.529 14.643 14.761 14.88
a730=48.6649 13.687 13.736 13.793 13.854 13.921 13.992 14.329 14.429 14.536 14.649 14.768 14.887
a731=48.7316 13.694 13.744 13.8 13.862 13.928 13.999 14.336 14.436 14.543 14.656 14.774 14.893
a732=48.7984 13.702 13.752 13.808 13.869 13.935 14.006 14.343 14.443 14.549 14.662 14.78 14.899
a733=48.8652 13.71 13.759 13.815 13.877 13.943 14.014 14.35 14.45 14.556 14.669 14.787 14.906
a734=48.9319 13.717 13.767 13.823 13.884 13.95 14.021 14.357 14.457 14.563 14.676 14.793 14.912
a735=48.9987 13.725 13.775 13.831 13.892 13.958 14.028 14.364 14.463 14.569 14.682 14.8 14.918
a736=49.0654 13.733 13.782 13.838 13.899 13.965 14.036 14.371 14.47 14.576 14.689 14.806 14.924
a737=49.1322 13.74 13.79 13.846 13.907 13.973 14.043 14.378 14.477 14.583 14.695 14.813 14.931
a738=49.1989 13.748 13.797 13.853 13.914 13.98 14.05 14.385 14.484 14.589 14.702 14.819 14.937
a739=49.2657 13.756 13.805 13.861 13.922 13.987 14.058 14.392 14.491 14.596 14.708 14.825 14.943
a740=49.3324 13.763 13.813 13.868 13.929 13.995 14.065 14.399 14.497 14.603 14.715 14.832 14.95
a741=49.3992 13.771 13.82 13.876 13.937 14.002 14.072 14.405 14.504 14.609 14.721 14.838 14.956
a742=49.466 13.779 13.828 13.883 13.944 14.009 14.079 14.412 14.511 14.616 14.728 14.845 14.962
a743=49.5327 13.786 13.835 13.891 13.952 14.017 14.087 14.419 14.518 14.623 14.734 14.851 14.968
a744=49.5995 13.794 13.843 13.898 13.959 14.024 14.094 14.426 14.524 14.629 14.741 14.857 14.975
a745=49.6662 13.802 13.85 13.906 13.966 14.031 14.101 14.433 14.531 14.636 14.747 14.864 14.981
a746=49.733 13.809 13.858 13.913 13.974 14.039 14.108 14.44 14.538 14.643 14.754 14.87 14.987
a747=49.7997 13.817 13.866 13.921 13.981 14.046 14.116 14.447 14.544 14.649 14.76 14.876 14.993
a748=49.8665 13.824 13.873 13.928 13.988 14.053 14.123 14.453 14.551 14.656 14.767 14.883 14.999
a749=49.9332 13.832 13.881 13.936 13.996 14.061 14.13 14.46 14.558 14.662 14.773 14.889 15.006
a750=50 13.84 13.888 13.943 14.003 14.068 14.137 14.467 14.565 14.669 14.78 14.895 15.012
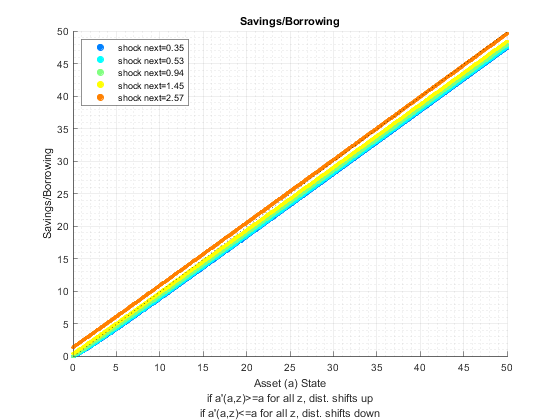
tb_pol_a: optimal asset choice for each state space point
z1_0_34741 z2_0_40076 z3_0_4623 z4_0_5333 z5_0_61519 z6_0_70966 z10_1_2567 z11_1_4496 z12_1_6723 z13_1_9291 z14_2_2253 z15_2_567
__________ __________ _________ _________ __________ __________ __________ __________ __________ __________ __________ _________
a1=0 0 0 0 0 0 0 0.20027 0.33378 0.53405 0.73431 1.0013 1.3351
a2=0.0667557 0 0 0 0 0 0 0.26702 0.40053 0.53405 0.80107 1.0681 1.4019
a3=0.133511 0 0 0 0 0.066756 0.066756 0.33378 0.46729 0.6008 0.86782 1.1348 1.4686
a4=0.200267 0.066756 0.066756 0.066756 0.066756 0.066756 0.066756 0.33378 0.53405 0.66756 0.93458 1.2016 1.5354
a5=0.267023 0.066756 0.066756 0.066756 0.066756 0.13351 0.13351 0.40053 0.53405 0.73431 1.0013 1.2684 1.6021
a6=0.333778 0.13351 0.13351 0.13351 0.13351 0.20027 0.20027 0.46729 0.6008 0.80107 1.0013 1.3351 1.6689
a7=0.400534 0.13351 0.20027 0.20027 0.20027 0.20027 0.26702 0.53405 0.66756 0.86782 1.0681 1.3351 1.7356
a8=0.46729 0.20027 0.20027 0.20027 0.20027 0.26702 0.26702 0.6008 0.73431 0.93458 1.1348 1.4019 1.7356
a9=0.534045 0.26702 0.26702 0.26702 0.26702 0.33378 0.33378 0.66756 0.80107 1.0013 1.2016 1.4686 1.8024
a10=0.600801 0.26702 0.33378 0.33378 0.33378 0.33378 0.40053 0.73431 0.86782 1.0681 1.2684 1.5354 1.8692
a11=0.667557 0.33378 0.33378 0.40053 0.40053 0.40053 0.46729 0.80107 0.93458 1.1348 1.3351 1.6021 1.9359
a12=0.734312 0.40053 0.40053 0.40053 0.46729 0.46729 0.53405 0.86782 1.0013 1.2016 1.4019 1.6689 2.0027
a13=0.801068 0.46729 0.46729 0.46729 0.46729 0.53405 0.53405 0.86782 1.0681 1.2684 1.4686 1.7356 2.0694
a14=0.867824 0.46729 0.53405 0.53405 0.53405 0.6008 0.6008 0.93458 1.1348 1.2684 1.5354 1.8024 2.1362
a15=0.934579 0.53405 0.53405 0.6008 0.6008 0.6008 0.66756 1.0013 1.2016 1.3351 1.6021 1.8692 2.2029
a16=1.00134 0.6008 0.6008 0.66756 0.66756 0.66756 0.73431 1.0681 1.2016 1.4019 1.6689 1.9359 2.2697
a17=1.06809 0.66756 0.66756 0.66756 0.73431 0.73431 0.80107 1.1348 1.2684 1.4686 1.7356 2.0027 2.3364
a18=1.13485 0.73431 0.73431 0.73431 0.73431 0.80107 0.86782 1.2016 1.3351 1.5354 1.8024 2.0694 2.4032
a19=1.2016 0.73431 0.80107 0.80107 0.80107 0.86782 0.86782 1.2684 1.4019 1.6021 1.8692 2.1362 2.47
a20=1.26836 0.80107 0.80107 0.86782 0.86782 0.93458 0.93458 1.3351 1.4686 1.6689 1.9359 2.2029 2.5367
a21=1.33511 0.86782 0.86782 0.93458 0.93458 1.0013 1.0013 1.4019 1.5354 1.7356 1.9359 2.2697 2.6035
a22=1.40187 0.93458 0.93458 0.93458 1.0013 1.0013 1.0681 1.4686 1.6021 1.8024 2.0027 2.3364 2.6702
a23=1.46862 1.0013 1.0013 1.0013 1.0681 1.0681 1.1348 1.5354 1.6689 1.8692 2.0694 2.4032 2.737
a24=1.53538 1.0681 1.0681 1.0681 1.1348 1.1348 1.2016 1.5354 1.7356 1.9359 2.1362 2.4032 2.8037
a25=1.60214 1.0681 1.1348 1.1348 1.1348 1.2016 1.2684 1.6021 1.8024 2.0027 2.2029 2.47 2.8037
a26=1.66889 1.1348 1.1348 1.2016 1.2016 1.2684 1.3351 1.6689 1.8692 2.0694 2.2697 2.5367 2.8705
a27=1.73565 1.2016 1.2016 1.2684 1.2684 1.3351 1.3351 1.7356 1.9359 2.1362 2.3364 2.6035 2.9372
a28=1.8024 1.2684 1.2684 1.3351 1.3351 1.4019 1.4019 1.8024 2.0027 2.1362 2.4032 2.6702 3.004
a29=1.86916 1.3351 1.3351 1.3351 1.4019 1.4019 1.4686 1.8692 2.0027 2.2029 2.47 2.737 3.0708
a30=1.93591 1.4019 1.4019 1.4019 1.4686 1.4686 1.5354 1.9359 2.0694 2.2697 2.5367 2.8037 3.1375
a31=2.00267 1.4019 1.4686 1.4686 1.5354 1.5354 1.6021 2.0027 2.1362 2.3364 2.6035 2.8705 3.2043
a32=2.06943 1.4686 1.5354 1.5354 1.5354 1.6021 1.6689 2.0694 2.2029 2.4032 2.6702 2.9372 3.271
a33=2.13618 1.5354 1.5354 1.6021 1.6021 1.6689 1.7356 2.1362 2.2697 2.47 2.737 3.004 3.3378
a34=2.20294 1.6021 1.6021 1.6689 1.6689 1.7356 1.8024 2.2029 2.3364 2.5367 2.8037 3.0708 3.4045
a35=2.26969 1.6689 1.6689 1.7356 1.7356 1.8024 1.8692 2.2697 2.4032 2.6035 2.8705 3.1375 3.4713
a36=2.33645 1.7356 1.7356 1.7356 1.8024 1.8692 1.8692 2.2697 2.47 2.6702 2.9372 3.2043 3.5381
a37=2.4032 1.8024 1.8024 1.8024 1.8692 1.9359 1.9359 2.3364 2.5367 2.737 2.9372 3.271 3.6048
a38=2.46996 1.8024 1.8692 1.8692 1.9359 1.9359 2.0027 2.4032 2.6035 2.8037 3.004 3.3378 3.6716
a39=2.53672 1.8692 1.9359 1.9359 2.0027 2.0027 2.0694 2.47 2.6702 2.8705 3.0708 3.4045 3.7383
a40=2.60347 1.9359 2.0027 2.0027 2.0694 2.0694 2.1362 2.5367 2.737 2.9372 3.1375 3.4713 3.8051
a41=2.67023 2.0027 2.0027 2.0694 2.0694 2.1362 2.2029 2.6035 2.8037 3.004 3.2043 3.4713 3.8718
a42=2.73698 2.0694 2.0694 2.1362 2.1362 2.2029 2.2697 2.6702 2.8705 3.0708 3.271 3.5381 3.9386
a43=2.80374 2.1362 2.1362 2.2029 2.2029 2.2697 2.3364 2.737 2.9372 3.0708 3.3378 3.6048 4.0053
a44=2.87049 2.2029 2.2029 2.2697 2.2697 2.3364 2.4032 2.8037 2.9372 3.1375 3.4045 3.6716 4.0721
a45=2.93725 2.2697 2.2697 2.2697 2.3364 2.4032 2.47 2.8705 3.004 3.2043 3.4713 3.7383 4.0721
a46=3.00401 2.3364 2.3364 2.3364 2.4032 2.47 2.5367 2.9372 3.0708 3.271 3.5381 3.8051 4.1389
a47=3.07076 2.3364 2.4032 2.4032 2.47 2.5367 2.5367 3.004 3.1375 3.3378 3.6048 3.8718 4.2056
a48=3.13752 2.4032 2.47 2.47 2.5367 2.5367 2.6035 3.0708 3.2043 3.4045 3.6716 3.9386 4.2724
a49=3.20427 2.47 2.5367 2.5367 2.6035 2.6035 2.6702 3.1375 3.271 3.4713 3.7383 4.0053 4.3391
a50=3.27103 2.5367 2.5367 2.6035 2.6702 2.6702 2.737 3.2043 3.3378 3.5381 3.8051 4.0721 4.4059
a701=46.729 44.192 44.192 44.259 44.326 44.393 44.526 44.993 45.194 45.461 45.728 46.061 46.395
a702=46.7957 44.259 44.259 44.326 44.393 44.459 44.526 45.06 45.26 45.527 45.794 46.061 46.462
a703=46.8625 44.326 44.326 44.393 44.459 44.526 44.593 45.127 45.327 45.594 45.861 46.128 46.529
a704=46.9292 44.393 44.393 44.459 44.526 44.593 44.66 45.194 45.394 45.661 45.928 46.195 46.595
a705=46.996 44.459 44.459 44.526 44.593 44.66 44.726 45.26 45.461 45.728 45.995 46.262 46.662
a706=47.0628 44.526 44.526 44.593 44.66 44.726 44.793 45.327 45.527 45.794 46.061 46.328 46.729
a707=47.1295 44.593 44.593 44.66 44.726 44.793 44.86 45.394 45.594 45.861 46.128 46.395 46.796
a708=47.1963 44.66 44.66 44.726 44.793 44.86 44.927 45.461 45.661 45.928 46.195 46.462 46.862
a709=47.263 44.726 44.726 44.793 44.86 44.927 44.993 45.527 45.728 45.995 46.262 46.529 46.929
a710=47.3298 44.726 44.793 44.86 44.927 44.993 45.06 45.594 45.794 46.061 46.328 46.595 46.996
a711=47.3965 44.793 44.86 44.927 44.993 45.06 45.127 45.661 45.861 46.061 46.395 46.662 47.063
a712=47.4633 44.86 44.927 44.993 45.06 45.127 45.194 45.728 45.928 46.128 46.395 46.729 47.13
a713=47.53 44.927 44.993 45.06 45.127 45.194 45.26 45.794 45.995 46.195 46.462 46.796 47.196
a714=47.5968 44.993 45.06 45.127 45.194 45.26 45.327 45.861 46.061 46.262 46.529 46.862 47.263
a715=47.6636 45.06 45.127 45.194 45.26 45.327 45.394 45.928 46.128 46.328 46.595 46.929 47.33
a716=47.7303 45.127 45.194 45.26 45.327 45.394 45.461 45.995 46.195 46.395 46.662 46.996 47.397
a717=47.7971 45.194 45.26 45.327 45.394 45.461 45.527 46.061 46.262 46.462 46.729 47.063 47.463
a718=47.8638 45.26 45.327 45.394 45.461 45.527 45.594 46.128 46.328 46.529 46.796 47.13 47.53
a719=47.9306 45.327 45.394 45.461 45.527 45.594 45.661 46.195 46.395 46.595 46.862 47.196 47.597
a720=47.9973 45.394 45.461 45.527 45.594 45.661 45.728 46.262 46.462 46.662 46.929 47.263 47.664
a721=48.0641 45.461 45.527 45.594 45.661 45.728 45.794 46.328 46.529 46.729 46.996 47.33 47.664
a722=48.1308 45.527 45.594 45.661 45.661 45.794 45.861 46.395 46.595 46.796 47.063 47.397 47.73
a723=48.1976 45.594 45.661 45.728 45.728 45.861 45.928 46.462 46.662 46.862 47.13 47.463 47.797
a724=48.2644 45.661 45.728 45.728 45.794 45.928 45.995 46.529 46.729 46.929 47.196 47.53 47.864
a725=48.3311 45.728 45.794 45.794 45.861 45.928 46.061 46.595 46.796 46.996 47.263 47.597 47.931
a726=48.3979 45.794 45.861 45.861 45.928 45.995 46.128 46.662 46.862 47.063 47.33 47.664 47.997
a727=48.4646 45.861 45.928 45.928 45.995 46.061 46.195 46.729 46.929 47.13 47.397 47.73 48.064
a728=48.5314 45.928 45.995 45.995 46.061 46.128 46.262 46.796 46.996 47.196 47.463 47.797 48.131
a729=48.5981 45.995 46.061 46.061 46.128 46.195 46.328 46.862 47.063 47.263 47.53 47.864 48.198
a730=48.6649 46.061 46.128 46.128 46.195 46.262 46.395 46.929 47.13 47.33 47.597 47.931 48.264
a731=48.7316 46.128 46.195 46.195 46.262 46.328 46.462 46.996 47.13 47.397 47.664 47.997 48.331
a732=48.7984 46.195 46.195 46.262 46.328 46.395 46.529 47.063 47.196 47.463 47.73 48.064 48.398
a733=48.8652 46.262 46.262 46.328 46.395 46.462 46.595 47.13 47.263 47.53 47.797 48.131 48.465
a734=48.9319 46.328 46.328 46.395 46.462 46.529 46.662 47.13 47.33 47.597 47.864 48.198 48.531
a735=48.9987 46.395 46.395 46.462 46.529 46.595 46.729 47.196 47.397 47.664 47.931 48.264 48.598
a736=49.0654 46.462 46.462 46.529 46.595 46.662 46.729 47.263 47.463 47.73 47.997 48.331 48.665
a737=49.1322 46.529 46.529 46.595 46.662 46.729 46.796 47.33 47.53 47.797 48.064 48.331 48.732
a738=49.1989 46.595 46.595 46.662 46.729 46.796 46.862 47.397 47.597 47.864 48.131 48.398 48.798
a739=49.2657 46.662 46.662 46.729 46.796 46.862 46.929 47.463 47.664 47.931 48.198 48.465 48.865
a740=49.3324 46.729 46.729 46.796 46.862 46.929 46.996 47.53 47.73 47.997 48.264 48.531 48.932
a741=49.3992 46.796 46.796 46.862 46.929 46.996 47.063 47.597 47.797 48.064 48.331 48.598 48.999
a742=49.466 46.862 46.862 46.929 46.996 47.063 47.13 47.664 47.864 48.131 48.398 48.665 49.065
a743=49.5327 46.929 46.929 46.996 47.063 47.13 47.196 47.73 47.931 48.198 48.465 48.732 49.132
a744=49.5995 46.929 46.996 47.063 47.13 47.196 47.263 47.797 47.997 48.264 48.531 48.798 49.199
a745=49.6662 46.996 47.063 47.13 47.196 47.263 47.33 47.864 48.064 48.331 48.598 48.865 49.266
a746=49.733 47.063 47.13 47.196 47.263 47.33 47.397 47.931 48.131 48.331 48.665 48.932 49.332
a747=49.7997 47.13 47.196 47.263 47.33 47.397 47.463 47.997 48.198 48.398 48.665 48.999 49.399
a748=49.8665 47.196 47.263 47.33 47.397 47.463 47.53 48.064 48.264 48.465 48.732 49.065 49.466
a749=49.9332 47.263 47.33 47.397 47.463 47.53 47.597 48.131 48.331 48.531 48.798 49.132 49.533
a750=50 47.33 47.397 47.463 47.53 47.597 47.664 48.198 48.398 48.598 48.865 49.199 49.599
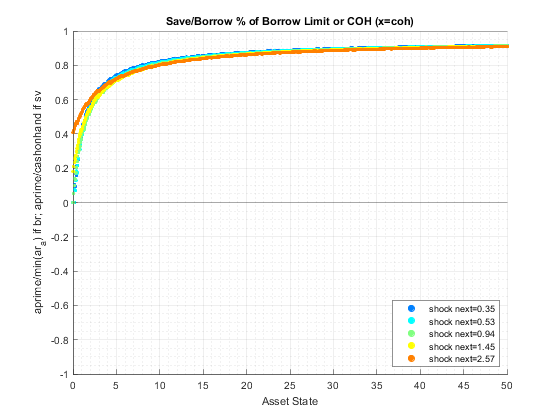
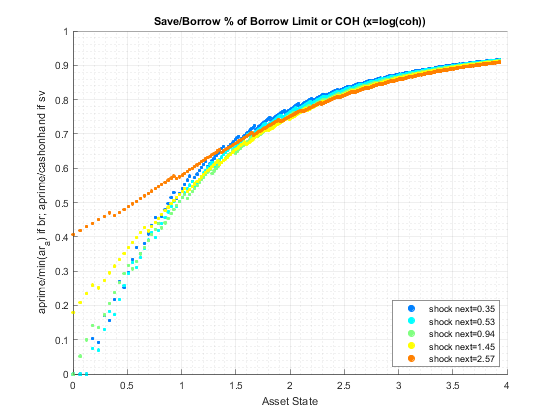
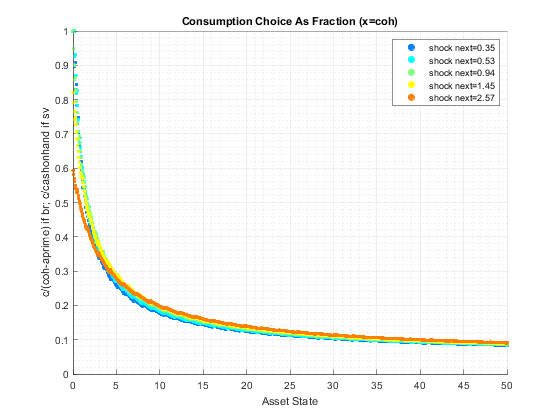
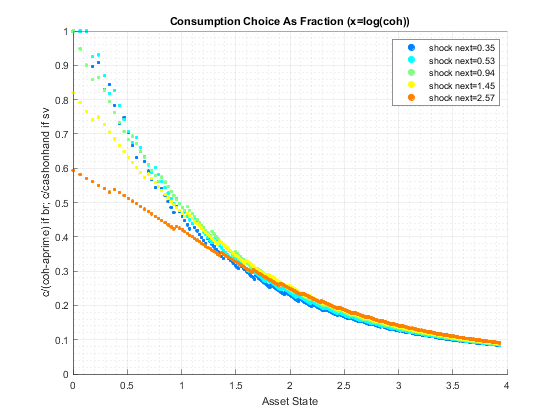
end
ans =
Map with properties:
Count: 12
KeyType: char
ValueType: any