Chapter 7 Optimization
7.1 Grid Based Optimization
7.1.1 Find Maximum By Iterating Over Grids
Go back to fan’s REconTools research support package, R4Econ examples page, PkgTestR packaging guide, or Stat4Econ course page.
7.1.1.1 Single Parameter Optimization
We have a function \(f(\mu)\), we know that \(a\le \mu \le b\), and we want to find the value of \(\mu\) that maximizes \(f(\mu)\) within the bounds. The same idea here is used in various aspects of solving the dynamic equilibrium borrowing and savings problem in Wang (2022) (preprint pdf).
First, we create a simple quadratic function. the minimum of the function is where \(\mu = -2\)
# Define Function
ffi_quad_func <- function(fl_mu) {
1 + (fl_mu + 2)^2
}
# Test Function
print(paste0("ffi_quad_func(-3)=", ffi_quad_func(-3)))## [1] "ffi_quad_func(-3)=2"## [1] "ffi_quad_func(-2)=1"## [1] "ffi_quad_func(-1)=2"Second, we develop the maximizer function given grid.
# Function
ffi_find_min <- function(fl_min = -4, fl_max = 2, it_grid_len = 7) {
# Construct grid where to evaluate the function
ar_fl_mu <- seq(fl_min, fl_max, length.out = it_grid_len)
# Evaluate likelihood
ar_obj <- sapply(ar_fl_mu, ffi_quad_func)
# Find min grid
it_min_idx <- which.min(ar_obj)
fl_min_val <- ar_obj[it_min_idx]
# Find lower and upper bound
fl_min_new <- ar_fl_mu[max(it_min_idx - 1, 1)]
fl_max_new <- ar_fl_mu[min(it_min_idx + 1, it_grid_len)]
# return
return(list(
fl_min_val = fl_min_val,
fl_min_new = fl_min_new,
fl_max_new = fl_max_new
))
}
# Test Function
print("ffi_find_min(-3,-1,10)")## [1] "ffi_find_min(-3,-1,10)"## $fl_min_val
## [1] 1.012346
##
## $fl_min_new
## [1] -2.333333
##
## $fl_max_new
## [1] -1.888889## [1] "ffi_find_min(-2,-1,10)"## $fl_min_val
## [1] 1
##
## $fl_min_new
## [1] -2
##
## $fl_max_new
## [1] -1.888889## [1] "ffi_find_min(-3,-2,10)"## $fl_min_val
## [1] 1
##
## $fl_min_new
## [1] -2.111111
##
## $fl_max_new
## [1] -2Third, we iterately zoom-in to ever finer grid around the point in the last grid where the objective function had the lowest value.
# Initialize min and max and tolerance criteria
fl_min_cur <- -10
fl_max_cur <- 10
it_grid_len <- 10
fl_tol <- 1e-5
it_max_iter <- 5
# Initialize initial gaps etc
fl_gap <- 1e5
fl_min_val_last <- 1e5
it_iter <- 0
# Iteratively loop over grid to find the maximum by zooming in
while ((fl_gap > fl_tol) && it_iter <= it_max_iter) {
# Iterator counts up
it_iter <- it_iter + 1
print(paste0("it_iter=", it_iter))
# build array
ls_find_min <- ffi_find_min(
fl_min = fl_min_cur, fl_max = fl_max_cur, it_grid_len = it_grid_len
)
# Min objective value current
fl_min_val <- ls_find_min$fl_min_val
# Find new lower and upper bound
fl_min_cur <- ls_find_min$fl_min_new
fl_max_cur <- ls_find_min$fl_max_new
print(paste0("fl_min_cur=", fl_min_cur))
print(paste0("fl_max_cur=", fl_max_cur))
# Compare
fl_gap <- abs(fl_min_val - fl_min_val_last)
fl_min_val_last <- fl_min_val
print(paste0("fl_gap=", fl_gap))
}## [1] "it_iter=1"
## [1] "fl_min_cur=-3.33333333333333"
## [1] "fl_max_cur=1.11111111111111"
## [1] "fl_gap=99998.2098765432"
## [1] "it_iter=2"
## [1] "fl_min_cur=-2.34567901234568"
## [1] "fl_max_cur=-1.35802469135802"
## [1] "fl_gap=0.768175582990399"
## [1] "it_iter=3"
## [1] "fl_min_cur=-2.12620027434842"
## [1] "fl_max_cur=-1.90672153635117"
## [1] "fl_gap=0.0216769123947906"
## [1] "it_iter=4"
## [1] "fl_min_cur=-2.02865416857186"
## [1] "fl_max_cur=-1.97988111568358"
## [1] "fl_gap=0.00025274863560476"
## [1] "it_iter=5"
## [1] "fl_min_cur=-2.00697725617707"
## [1] "fl_max_cur=-1.99613879997968"
## [1] "fl_gap=1.57853178373024e-05"
## [1] "it_iter=6"
## [1] "fl_min_cur=-2.00095589162296"
## [1] "fl_max_cur=-1.99854734580132"
## [1] "fl_gap=2.36575822887275e-06"7.1.2 Bisection
Go back to fan’s REconTools research support package, R4Econ examples page, PkgTestR packaging guide, or Stat4Econ course page.
See the ff_opti_bisect_pmap_multi function from Fan’s REconTools Package, which provides a resuable function based on the algorithm worked out here.
The bisection specific code does not need to do much.
- list variables in file for grouping, each group is an individual for whom we want to calculate optimal choice for using bisection.
- string variable name of input where functions are evaluated, these are already contained in the dataframe, existing variable names, row specific, rowwise computation over these, each rowwise calculation using different rows.
- scalar and array values that are applied to every rowwise calculation, all rowwise calculations using the same scalars and arrays.
- string output variable name
This is how I implement the bisection algorithm, when we know the bounding minimum and maximum to be below and above zero already.
- Evaluate \(f^0_a = f(a^0)\) and \(f^0_b = f(b^0)\), min and max points.
- Evaluate at \(f^0_p = f(p^0)\), where \(p_0 = \frac{a^0+b^0}{2}\).
- if \(f^i_a \cdot f^i_p < 0\), then \(b_{i+1} = p_i\), else, \(a_{i+1} = p_i\) and \(f^{i+1}_a = p_i\).
- iteratre until convergence.
Generate New columns of a and b as we iteratre, do not need to store p, p is temporary. Evaluate the function below which we have already tested, but now, in the dataframe before generating all permutations, tb_states_choices, now the fl_N element will be changing with each iteration, it will be row specific. fl_N are first min and max, then each subsequent ps.
7.1.2.1 Initialize Matrix
Prepare Input Data:
# Parameters
fl_rho = 0.20
svr_id_var = 'INDI_ID'
# P fixed parameters, nN is N dimensional, nP is P dimensional
ar_nN_A = seq(-2, 2, length.out = 4)
ar_nN_alpha = seq(0.1, 0.9, length.out = 4)
# Choice Grid for nutritional feasible choices for each
fl_N_agg = 100
fl_N_min = 0
# Mesh Expand
tb_states_choices <- as_tibble(cbind(ar_nN_A, ar_nN_alpha)) %>%
rowid_to_column(var=svr_id_var)
# Convert Matrix to Tibble
ar_st_col_names = c(svr_id_var,'fl_A', 'fl_alpha')
tb_states_choices <- tb_states_choices %>% rename_all(~c(ar_st_col_names))Prepare Function:
# Define Implicit Function
ffi_nonlin_dplyrdo <- function(fl_A, fl_alpha, fl_N, ar_A, ar_alpha, fl_N_agg, fl_rho){
ar_p1_s1 = exp((fl_A - ar_A)*fl_rho)
ar_p1_s2 = (fl_alpha/ar_alpha)
ar_p1_s3 = (1/(ar_alpha*fl_rho - 1))
ar_p1 = (ar_p1_s1*ar_p1_s2)^ar_p1_s3
ar_p2 = fl_N^((fl_alpha*fl_rho-1)/(ar_alpha*fl_rho-1))
ar_overall = ar_p1*ar_p2
fl_overall = fl_N_agg - sum(ar_overall)
return(fl_overall)
}Initialize the matrix with \(a_0\) and \(b_0\), the initial min and max points:
# common prefix to make reshaping easier
st_bisec_prefix <- 'bisec_'
svr_a_lst <- paste0(st_bisec_prefix, 'a_0')
svr_b_lst <- paste0(st_bisec_prefix, 'b_0')
svr_fa_lst <- paste0(st_bisec_prefix, 'fa_0')
svr_fb_lst <- paste0(st_bisec_prefix, 'fb_0')
# Add initial a and b
tb_states_choices_bisec <- tb_states_choices %>%
mutate(!!sym(svr_a_lst) := fl_N_min, !!sym(svr_b_lst) := fl_N_agg)
# Evaluate function f(a_0) and f(b_0)
tb_states_choices_bisec <- tb_states_choices_bisec %>%
rowwise() %>%
mutate(!!sym(svr_fa_lst) := ffi_nonlin_dplyrdo(fl_A, fl_alpha, !!sym(svr_a_lst),
ar_nN_A, ar_nN_alpha,
fl_N_agg, fl_rho),
!!sym(svr_fb_lst) := ffi_nonlin_dplyrdo(fl_A, fl_alpha, !!sym(svr_b_lst),
ar_nN_A, ar_nN_alpha,
fl_N_agg, fl_rho))
# Summarize
dim(tb_states_choices_bisec)## [1] 4 77.1.2.2 Iterate and Solve for f(p), update f(a) and f(b)
Implement the DPLYR based Concurrent bisection algorithm.
# fl_tol = float tolerance criteria
# it_tol = number of interations to allow at most
fl_tol <- 10^-2
it_tol <- 100
# fl_p_dist2zr = distance to zero to initalize
fl_p_dist2zr <- 1000
it_cur <- 0
while (it_cur <= it_tol && fl_p_dist2zr >= fl_tol ) {
it_cur <- it_cur + 1
# New Variables
svr_a_cur <- paste0(st_bisec_prefix, 'a_', it_cur)
svr_b_cur <- paste0(st_bisec_prefix, 'b_', it_cur)
svr_fa_cur <- paste0(st_bisec_prefix, 'fa_', it_cur)
svr_fb_cur <- paste0(st_bisec_prefix, 'fb_', it_cur)
# Evaluate function f(a_0) and f(b_0)
# 1. generate p
# 2. generate f_p
# 3. generate f_p*f_a
tb_states_choices_bisec <- tb_states_choices_bisec %>%
rowwise() %>%
mutate(p = ((!!sym(svr_a_lst) + !!sym(svr_b_lst))/2)) %>%
mutate(f_p = ffi_nonlin_dplyrdo(fl_A, fl_alpha, p,
ar_nN_A, ar_nN_alpha,
fl_N_agg, fl_rho)) %>%
mutate(f_p_t_f_a = f_p*!!sym(svr_fa_lst))
# fl_p_dist2zr = sum(abs(p))
fl_p_dist2zr <- mean(abs(tb_states_choices_bisec %>% pull(f_p)))
# Update a and b
tb_states_choices_bisec <- tb_states_choices_bisec %>%
mutate(!!sym(svr_a_cur) :=
case_when(f_p_t_f_a < 0 ~ !!sym(svr_a_lst),
TRUE ~ p)) %>%
mutate(!!sym(svr_b_cur) :=
case_when(f_p_t_f_a < 0 ~ p,
TRUE ~ !!sym(svr_b_lst)))
# Update f(a) and f(b)
tb_states_choices_bisec <- tb_states_choices_bisec %>%
mutate(!!sym(svr_fa_cur) :=
case_when(f_p_t_f_a < 0 ~ !!sym(svr_fa_lst),
TRUE ~ f_p)) %>%
mutate(!!sym(svr_fb_cur) :=
case_when(f_p_t_f_a < 0 ~ f_p,
TRUE ~ !!sym(svr_fb_lst)))
# Save from last
svr_a_lst <- svr_a_cur
svr_b_lst <- svr_b_cur
svr_fa_lst <- svr_fa_cur
svr_fb_lst <- svr_fb_cur
# Summar current round
print(paste0('it_cur:', it_cur, ', fl_p_dist2zr:', fl_p_dist2zr))
summary(tb_states_choices_bisec %>%
select(one_of(svr_a_cur, svr_b_cur, svr_fa_cur, svr_fb_cur)))
}## [1] "it_cur:1, fl_p_dist2zr:1597.93916362849"
## [1] "it_cur:2, fl_p_dist2zr:676.06602535902"
## [1] "it_cur:3, fl_p_dist2zr:286.850590132782"
## [1] "it_cur:4, fl_p_dist2zr:117.225493866655"
## [1] "it_cur:5, fl_p_dist2zr:37.570593471664"
## [1] "it_cur:6, fl_p_dist2zr:4.60826664896022"
## [1] "it_cur:7, fl_p_dist2zr:14.4217689135683"
## [1] "it_cur:8, fl_p_dist2zr:8.38950830086659"
## [1] "it_cur:9, fl_p_dist2zr:3.93347761455868"
## [1] "it_cur:10, fl_p_dist2zr:1.88261338941038"
## [1] "it_cur:11, fl_p_dist2zr:0.744478952222305"
## [1] "it_cur:12, fl_p_dist2zr:0.187061801237917"
## [1] "it_cur:13, fl_p_dist2zr:0.117844913432613"
## [1] "it_cur:14, fl_p_dist2zr:0.0275365951418891"
## [1] "it_cur:15, fl_p_dist2zr:0.0515488156908255"
## [1] "it_cur:16, fl_p_dist2zr:0.0191152349149135"
## [1] "it_cur:17, fl_p_dist2zr:0.00385372194545752"7.1.2.3 Reshape Wide to long to Wide
To view results easily, how iterations improved to help us find the roots, convert table from wide to long. Pivot twice. This allows us to easily graph out how bisection is working out iterationby iteration.
Here, we will first show what the raw table looks like, the wide only table, and then show the long version, and finally the version that is medium wide.
7.1.2.3.1 Table One–Very Wide
Show what the tb_states_choices_bisec looks like.
Variables are formatted like: bisec_xx_yy, where yy is the iteration indicator, and xx is either a, b, fa, or fb.
| INDI_ID | 1.000000e+00 | 2.0000000 | 3.0000000 | 4.0000000 |
| fl_A | -2.000000e+00 | -0.6666667 | 0.6666667 | 2.0000000 |
| fl_alpha | 1.000000e-01 | 0.3666667 | 0.6333333 | 0.9000000 |
| bisec_a_0 | 0.000000e+00 | 0.0000000 | 0.0000000 | 0.0000000 |
| bisec_b_0 | 1.000000e+02 | 100.0000000 | 100.0000000 | 100.0000000 |
| bisec_fa_0 | 1.000000e+02 | 100.0000000 | 100.0000000 | 100.0000000 |
| bisec_fb_0 | -1.288028e+04 | -1394.7069782 | -323.9421599 | -51.9716069 |
| p | 1.544952e+00 | 8.5838318 | 24.8359680 | 65.0367737 |
| f_p | -7.637200e-03 | -0.0052211 | -0.0016162 | -0.0009405 |
| f_p_t_f_a | -3.800000e-04 | -0.0000237 | -0.0000025 | -0.0000002 |
| bisec_a_1 | 0.000000e+00 | 0.0000000 | 0.0000000 | 50.0000000 |
| bisec_b_1 | 5.000000e+01 | 50.0000000 | 50.0000000 | 100.0000000 |
| bisec_fa_1 | 1.000000e+02 | 100.0000000 | 100.0000000 | 22.5557704 |
| bisec_fb_1 | -5.666956e+03 | -595.7345364 | -106.5105843 | -51.9716069 |
| bisec_a_2 | 0.000000e+00 | 0.0000000 | 0.0000000 | 50.0000000 |
| bisec_b_2 | 2.500000e+01 | 25.0000000 | 25.0000000 | 75.0000000 |
| bisec_fa_2 | 1.000000e+02 | 100.0000000 | 100.0000000 | 22.5557704 |
| bisec_fb_2 | -2.464562e+03 | -224.1460032 | -0.6857375 | -14.8701831 |
| bisec_a_3 | 0.000000e+00 | 0.0000000 | 12.5000000 | 62.5000000 |
| bisec_b_3 | 1.250000e+01 | 12.5000000 | 25.0000000 | 75.0000000 |
| bisec_fa_3 | 1.000000e+02 | 100.0000000 | 50.8640414 | 3.7940196 |
| bisec_fb_3 | -1.041574e+03 | -51.1700464 | -0.6857375 | -14.8701831 |
| bisec_a_4 | 0.000000e+00 | 6.2500000 | 18.7500000 | 62.5000000 |
| bisec_b_4 | 6.250000e+00 | 12.5000000 | 25.0000000 | 68.7500000 |
| bisec_fa_4 | 1.000000e+02 | 29.4271641 | 25.2510409 | 3.7940196 |
7.1.2.3.2 Table Two–Very Wide to Very Long
We want to treat the iteration count information that is the suffix of variable names as a variable by itself. Additionally, we want to treat the a,b,fa,fb as a variable. Structuring the data very long like this allows for easy graphing and other types of analysis. Rather than dealing with many many variables, we have only 3 core variables that store bisection iteration information.
Here we use the very nice pivot_longer function. Note that to achieve this, we put a common prefix in front of the variables we wanted to convert to long. THis is helpful, because we can easily identify which variables need to be reshaped.
# New variables
svr_bisect_iter <- 'biseciter'
svr_abfafb_long_name <- 'varname'
svr_number_col <- 'value'
svr_id_bisect_iter <- paste0(svr_id_var, '_bisect_ier')
# Pivot wide to very long
tb_states_choices_bisec_long <- tb_states_choices_bisec %>%
pivot_longer(
cols = starts_with(st_bisec_prefix),
names_to = c(svr_abfafb_long_name, svr_bisect_iter),
names_pattern = paste0(st_bisec_prefix, "(.*)_(.*)"),
values_to = svr_number_col
)
# Print
# summary(tb_states_choices_bisec_long)
kable(head(tb_states_choices_bisec_long %>%
select(-one_of('p','f_p','f_p_t_f_a')), 15)) %>%
kable_styling_fc()| INDI_ID | fl_A | fl_alpha | varname | biseciter | value |
|---|---|---|---|---|---|
| 1 | -2 | 0.1 | a | 0 | 0.000 |
| 1 | -2 | 0.1 | b | 0 | 100.000 |
| 1 | -2 | 0.1 | fa | 0 | 100.000 |
| 1 | -2 | 0.1 | fb | 0 | -12880.284 |
| 1 | -2 | 0.1 | a | 1 | 0.000 |
| 1 | -2 | 0.1 | b | 1 | 50.000 |
| 1 | -2 | 0.1 | fa | 1 | 100.000 |
| 1 | -2 | 0.1 | fb | 1 | -5666.956 |
| 1 | -2 | 0.1 | a | 2 | 0.000 |
| 1 | -2 | 0.1 | b | 2 | 25.000 |
| 1 | -2 | 0.1 | fa | 2 | 100.000 |
| 1 | -2 | 0.1 | fb | 2 | -2464.562 |
| 1 | -2 | 0.1 | a | 3 | 0.000 |
| 1 | -2 | 0.1 | b | 3 | 12.500 |
| 1 | -2 | 0.1 | fa | 3 | 100.000 |
kable(tail(tb_states_choices_bisec_long %>%
select(-one_of('p','f_p','f_p_t_f_a')), 15)) %>%
kable_styling_fc()| INDI_ID | fl_A | fl_alpha | varname | biseciter | value |
|---|---|---|---|---|---|
| 4 | 2 | 0.9 | b | 14 | 65.0390625 |
| 4 | 2 | 0.9 | fa | 14 | 0.0047633 |
| 4 | 2 | 0.9 | fb | 14 | -0.0043628 |
| 4 | 2 | 0.9 | a | 15 | 65.0360107 |
| 4 | 2 | 0.9 | b | 15 | 65.0390625 |
| 4 | 2 | 0.9 | fa | 15 | 0.0002003 |
| 4 | 2 | 0.9 | fb | 15 | -0.0043628 |
| 4 | 2 | 0.9 | a | 16 | 65.0360107 |
| 4 | 2 | 0.9 | b | 16 | 65.0375366 |
| 4 | 2 | 0.9 | fa | 16 | 0.0002003 |
| 4 | 2 | 0.9 | fb | 16 | -0.0020812 |
| 4 | 2 | 0.9 | a | 17 | 65.0360107 |
| 4 | 2 | 0.9 | b | 17 | 65.0367737 |
| 4 | 2 | 0.9 | fa | 17 | 0.0002003 |
| 4 | 2 | 0.9 | fb | 17 | -0.0009405 |
7.1.2.3.3 Table Two–Very Very Long to Wider Again
But the previous results are too long, with the a, b, fa, and fb all in one column as different categories, they are really not different categories, they are in fact different types of variables. So we want to spread those four categories of this variable into four columns, each one representing the a, b, fa, and fb values. The rows would then be uniquly identified by the iteration counter and individual ID.
# Pivot wide to very long to a little wide
tb_states_choices_bisec_wider <- tb_states_choices_bisec_long %>%
pivot_wider(
names_from = !!sym(svr_abfafb_long_name),
values_from = svr_number_col
)
# Print
# summary(tb_states_choices_bisec_wider)
kable(head(tb_states_choices_bisec_wider %>%
select(-one_of('p','f_p','f_p_t_f_a')), 10)) %>%
kable_styling_fc_wide()| INDI_ID | fl_A | fl_alpha | biseciter | a | b | fa | fb |
|---|---|---|---|---|---|---|---|
| 1 | -2 | 0.1 | 0 | 0.000000 | 100.0000 | 100.00000 | -12880.283918 |
| 1 | -2 | 0.1 | 1 | 0.000000 | 50.0000 | 100.00000 | -5666.955763 |
| 1 | -2 | 0.1 | 2 | 0.000000 | 25.0000 | 100.00000 | -2464.562178 |
| 1 | -2 | 0.1 | 3 | 0.000000 | 12.5000 | 100.00000 | -1041.574253 |
| 1 | -2 | 0.1 | 4 | 0.000000 | 6.2500 | 100.00000 | -408.674764 |
| 1 | -2 | 0.1 | 5 | 0.000000 | 3.1250 | 100.00000 | -126.904283 |
| 1 | -2 | 0.1 | 6 | 0.000000 | 1.5625 | 100.00000 | -1.328965 |
| 1 | -2 | 0.1 | 7 | 0.781250 | 1.5625 | 54.69612 | -1.328965 |
| 1 | -2 | 0.1 | 8 | 1.171875 | 1.5625 | 27.46061 | -1.328965 |
| 1 | -2 | 0.1 | 9 | 1.367188 | 1.5625 | 13.23495 | -1.328965 |
kable(head(tb_states_choices_bisec_wider %>%
select(-one_of('p','f_p','f_p_t_f_a')), 10)) %>%
kable_styling_fc_wide()| INDI_ID | fl_A | fl_alpha | biseciter | a | b | fa | fb |
|---|---|---|---|---|---|---|---|
| 1 | -2 | 0.1 | 0 | 0.000000 | 100.0000 | 100.00000 | -12880.283918 |
| 1 | -2 | 0.1 | 1 | 0.000000 | 50.0000 | 100.00000 | -5666.955763 |
| 1 | -2 | 0.1 | 2 | 0.000000 | 25.0000 | 100.00000 | -2464.562178 |
| 1 | -2 | 0.1 | 3 | 0.000000 | 12.5000 | 100.00000 | -1041.574253 |
| 1 | -2 | 0.1 | 4 | 0.000000 | 6.2500 | 100.00000 | -408.674764 |
| 1 | -2 | 0.1 | 5 | 0.000000 | 3.1250 | 100.00000 | -126.904283 |
| 1 | -2 | 0.1 | 6 | 0.000000 | 1.5625 | 100.00000 | -1.328965 |
| 1 | -2 | 0.1 | 7 | 0.781250 | 1.5625 | 54.69612 | -1.328965 |
| 1 | -2 | 0.1 | 8 | 1.171875 | 1.5625 | 27.46061 | -1.328965 |
| 1 | -2 | 0.1 | 9 | 1.367188 | 1.5625 | 13.23495 | -1.328965 |
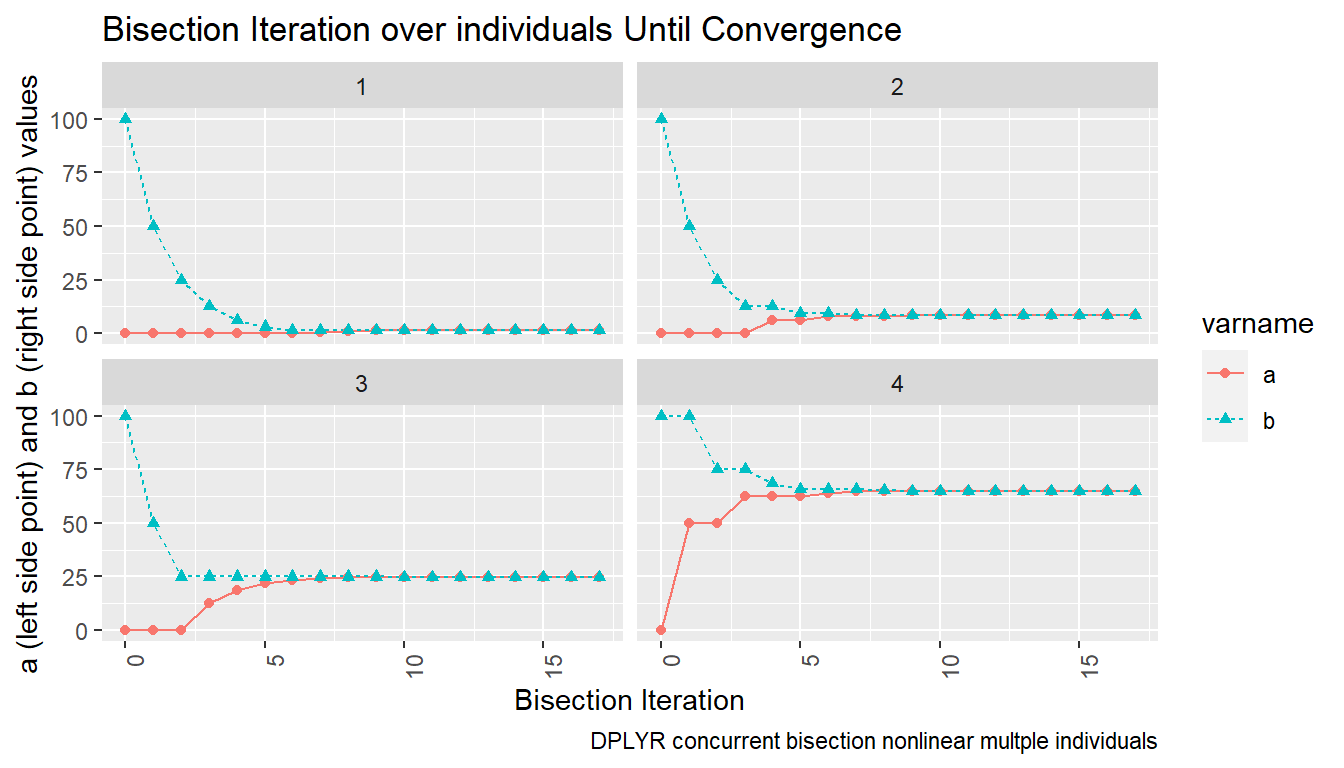
7.1.2.4 Graph Bisection Iteration Results
Actually we want to graph based on the long results, not the wider. Wider easier to view in table.
# Graph results
lineplot <- tb_states_choices_bisec_long %>%
mutate(!!sym(svr_bisect_iter) := as.numeric(!!sym(svr_bisect_iter))) %>%
filter(!!sym(svr_abfafb_long_name) %in% c('a', 'b')) %>%
ggplot(aes(x=!!sym(svr_bisect_iter), y=!!sym(svr_number_col),
colour=!!sym(svr_abfafb_long_name),
linetype=!!sym(svr_abfafb_long_name),
shape=!!sym(svr_abfafb_long_name))) +
facet_wrap( ~ INDI_ID) +
geom_line() +
geom_point() +
labs(title = 'Bisection Iteration over individuals Until Convergence',
x = 'Bisection Iteration',
y = 'a (left side point) and b (right side point) values',
caption = 'DPLYR concurrent bisection nonlinear multple individuals') +
theme(axis.text.x = element_text(angle = 90, hjust = 1))
print(lineplot)